Geometrisches in 2D Spielwelten
Schnitt von Strecken
Der Schnitt von Strecken ist ein elementares geometrisches Problem. Er wird hier behandelt nach einem
Vorschlag von Robert Sedgewick. Zunächst werden
die prinzipiellen Anordnungsmöglichkeiten der Strecken betrachtet. Es lassen sich folgende Fälle unterscheiden:
-
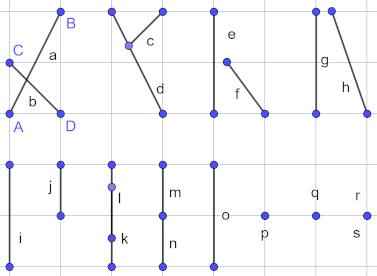
- Schnitte von Strecken
- a und b haben einen gemeinsamen Schnittpunkt innerhalb von a bzw. b.
- Der Streckenstart von c liegt innerhalb von d.
- Der Strahl von f erzeugt einen Schnitt innerhalb von e.
- Der Strahlen von g und h erzeugt einen Schnitt außerhalb von g und h.
- i und j sind parallel.
- l und k sind parallel und überschneiden sich vollständig oder teilweise.
- m ist im Gegensatz zu n auf einen Punkt auf n reduziert.
- p ist im Gegensatz zu o auf einen Punkt außerhalb von o reduziert.
- beide Strecken p und q sind auf verschiedene Punkte reduziert.
- beide Strecken r und s sind auf einen Punkt reduziert.
Eine Möglichkeit die Schnittpunkte der Strecken zu bestimmen liegt darin, die Gradengleichungen zu ermitteln,
die Schnittpunkte zu berechnen und anschließend zu prüfen, ob die Schnittpunkte auf den Strecken liegen.
Dabei müssten dann aber die Sonderfälle Strecke ist auf einen Punkt reduziert und Strecke ist senkrecht
geeignet behandelt werden.
Vorteilhafter ist es, sich zunächst eine Hilfsfunktion IsCounterClockwise(Point: p0, p1, p1) zu bauen.
Diese Funktion beantwortet die Frage, ob der Weg von p0 nach p1 nach p2 im oder
gegen den Uhrzeigersinn verläuft. Z.B. verläuft der Weg A, C, B im Uhrzeigersinn, der Weg D, B, C gegen den Uhrzeigersinn.

Letztendlich vergleicht IsCounterClockwise die Steigungen der Strecken,
die p1 und p0 bzw. p2 und p0 verbinden. m1 = dy1/dx1 ist die Steigung der ersten,
m2 = dy2/dx2 die der zweiten Strecke. Falls m1 < m2 ist eine Drehung gegen
den Uhrzeigersinn nötig, um von p0 über p1 nach p2 zu kommen ansonsten andersherum.
Im Programm werden aber m1 und m2 nicht direkt verglichen, da die Strecken auch
senkrecht stehen können (Division durch 0). Durch Multiplikation mit dx1 * dx2 wird dieses
Problem umgangen.
Bleibt die Frage zu klären, was passiert, wenn die Steigungen alle gleich, d.h. die Punkte
kolinear, sind.
Die Funktion IsCounterClockwise ist dreiwertig. Sie gibt 1 bzw. -1 oder 0 zurück.
Aus praktischen Gründen wird vereinbart, daß falls
- p0 zwischen p2 und p1 liegt, -1
- p2 zwischen p0 und p1 liegt, 0
- p1 zwischen p0 und p2 liegt, 1
zurückgegeben wird.
Um jetzt die ursprüngliche Frage zu beantworten kommt die Funktion Intersect(Point: polyStart, polyEnd, testStart, testEnd) ins Spiel.
Die Strecken schneiden sich, falls sich die jeweiligen Start- und Endpunkte der einen Strecke auf unterschiedlichen 'Seiten' der anderen
Strecke befinden.
Punkt in Polygon
-
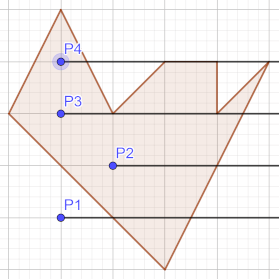
- Punkt in Polygon
Mit Hilfe der oben beschrieben Funktionen kann jetzt eine Methode entwickelt werden,
die feststellen kann, ob sich ein Punkt in einem geschlossenem Polygon befindet oder nicht.
Die Grundidee besteht darin, vom Punkt aus eine Line zu ziehen, deren Ende sicher außerhalb des
Polygons liegt. Im Anschluß wird die Anzahl der Schnitte der Testlinie mit dem Polygon bestimmt.
Ist diese Zahl gerade, liegt der Punkt außerhalb ansonsten innerhalb des Polygons (siehe P1 und P2).
Leider ist das in bestimmten Situationen problematisch (siehe P3 und P4). Es ist weder klar, wie
ein Schnitt der Testlinie mit einem Eckpunkt des Polygons, noch wie die Überlagerung der
Testlinie mit einem Polygonsegment, gezählt werden kann.
Diese Klippe wird umschifft, indem die Grundidee leicht abgewandelt wird. Das Polygon wird
umlaufen. Dabei wird gezählt, wie oft die Testlinie überquert wird. D.h. Punkte auf
der Testlinie werden ignoriert. Eine gerade Anzahl Seitenwechsel bedeutet außerhalb,
eine ungerade innerhalb.


