Elemente der Datenstruktur Baum

Bäume sind wichtige Datenstrukturen in der Informatik.
Bäume sind Graphen mit speziellen Eigenschaften. Wie Graphen bestehen sie aus Knoten und Kanten.
Kanten verbinden Knoten. Anders als Graphen sind Bäume immer gerichtet und enthalten niemals Kreise
d.h es gibt genau einen Weg von der Wurzel zum Knoten. Bäume bilden eine Hierarchie ab.
Die hier am Beispiel eines binären Baumes erläuterten Begriffe gelten für alle Bäume.
Die Elemente
-
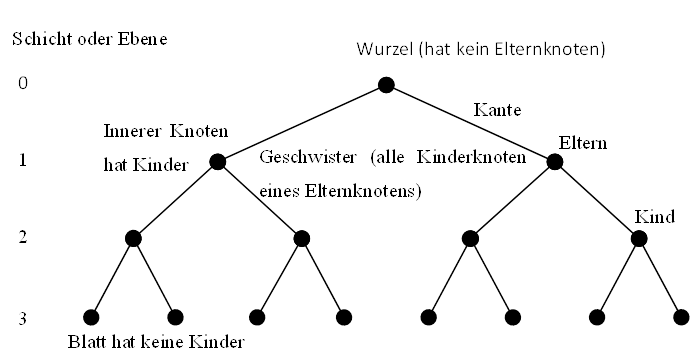
- Binär Baum
- Ein Baum
- ist eine Datenstruktur mit genau einem Knoten (Wurzel) ohne Eltern und sonstigen Knoten mit genau einem Elternknoten.
- Eine Kante
- verbindet zwei Knoten in hierarchischer Beziehung.
- Eltern Kind Knoten
- sind Knoten in direkter (hierarchischer) Folge.
- Innere Knoten
- sind alle Knoten mit mindestens einem Nachfolger (Kind).
- Ein Blatt
- ist ein Knoten ohne Nachfolger (Kind).
- Der Grad
- eines Baumes entspricht der höchsten Kinderzahl (Verzweigungsgrad) eines Elternknotens.
- Ein Binärbaum
- hat den Grad 2.
- Die Ebenen
- eines Baumes werden 0 basiert von der Wurzel aus gezählt. Knoten direkter Folge haben eine Ebenendifferenz von 1.
- Die Höhe
- eines Baumes ist seine tiefste Ebene.
- Die Weglänge
- ist die Zahl der Kanten von der Wurzel bis zum entsprechenden Knoten. Sie entspricht seiner Ebene.
- Im ausgeglichenem Baum
- ist die max. Differenz der Weglängen aller Blätter ± 1.
Bäume können in unterschiedlicher Weise implementiert werden. Zum Beispiel als mit Verweisen verkettete Knotenobjekte oder als Array in dem der Feldindex zur 'Verkettung' genutzt wird.

