Autonomer Boid - Verhalten in einer 2D Welt

Hier wird gezeigt, wie die 2D Steuerung autonomer Charaktäre in animierten Spielen realisiert werden kann. Die Umsetzung beruht in weiten Teilen auf Ideen von Craig Reynolds. Die Beispiele beziehen sich auf ein einfaches Boidmodell. Gerechnet wird in SI Einheiten also Kilogramm, Meter, Sekunde, Newton usw.. Winkel werden in Radiant(-PI, PI) angegeben. Positive Winkel werden gegen den Uhrzeigersinn gemessen/berechnet. Das Koordinatensystem hat nach oben zunehmende Y - Werte und nach rechts zunehmende X - Werte, ist also nicht identisch mit den üblichen Bildschirmkoordinaten. Da es um Verhalten in einer 2D Welt geht, werden nur 2D Vektoren genutzt.
Ziel ist die Berechnung 'glaubwürdiger' Bewegungen in einem System, das bei Bedarf um physikalische Eigenschaften (z.B. Reibung, Drehmoment etc.) erweitert werden kann. Gesteuert wird der Boid durch die einwirkende Kraft.

Bewegung des Boids

Grundlage der Positionsberechnung sind drei Gleichungen der klassischen Newtonschen Mechanik. Sie beschreiben den Zusammenhang von:

• Kraft, Masse und Beschleunigung: F = m * a
• Geschwindigkeit, Beschleunigung und Zeit: v = v₀ + a * t
• Ort, Geschwindigkeit und Zeit: p = p₀ + v * t

Das Boid Basismodell besteht aus:

• Vector steeringForce // aktuelle Kraft in Newton
• double mass // Masse in kg
• Vector position // Meter im Weltkoordinatensystem
• double maxVelocity // maximale Geschwindigkeit in Meter pro Sekunde
• Vector velocity // aktuelle Geschwindigkeit in Meter pro Sekunde
• double heading // aktuelle Ausrichtung des Boids in +Pi to -Pi als Atan2(velocity)

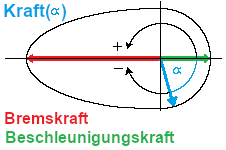
Asymmetrische Kraftellipse

Zur Berechnung der Beschleunigungskraft wird eine asymmetrische Ellipse benutzt. So kann dem Umstand, daß Bremswege im Allgemeinen kürzer als Beschleunigungswege und Kurvenradien bei niederiger Geschwindigkeit im Allgemeinen kleiner als bei größerer Geschwindigkeit sind, Rechnung getragen werden. Parameter zur Erzeugung der Ellipse sind:

• double maxAccelerationForce // die Beschleunigungskraft (große Halbachse beim Beschleunigen)
• double maxDecelerationForce // die Bremskraft (große Halbachse beim Bremsen) >= Beschleunigungskraft
• double actSteeringFactor // der Parameter (kleine Halbachse)<= Bremskraft

Keiner dieser Parameter muss konstant sein. Speziell der dritte Parameter kann (sollte) dynamisch bestimmt werden, um die 'Wendigkeit' des Boids geschwindigkeitsabhängig zu gestalten. Zur Berechnung der Kraft wird die Mittelpunktsform ( Polarkoordinaten) der Ellipsengleichung verwendet. Die Funktion GetSteeringForce berechnet den Kraftvektor aus dem Vektor zum Ziel und der gewünschten Geschwindigkeit.

Sobald die Kraft berechnet ist, kann die Geschwindigkeit und Position neu berechnet werden.

Die verschiedenen Verhalten des Boids zu implementieren reduziert sich jetzt darauf, einen geeigneten toTarget Vektor und eine geeignete Geschwindigkeit zu bestimmen.

Der Boid steuert ein Ziel an

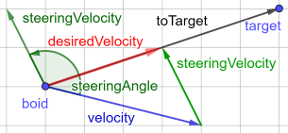
Vektoren für die Suche

Der Boid hat ein Ziel erkannt und soll es (möglichst schnell) ansteuern. D.h. Der Abstand zur aktuellen Position des Ziels soll minimiert werden. Um dies zu erreichen, müssen

1. der Richtungsvektor zum Ziel mit: toTarget = target.postition - position
2. die gewünschte Geschwindigkeit mit: desiredSpeed = maxVelocity

bestimmt werden.

Der Boid wird das Ziel mit Maximalgeschwindigkeit rammen und sich über das Ziel hinaus bewegen oder in manchen Fällen, abhängig von seiner Wendigkeit und der Targetgeschwindigkeit, umkreisen. Diesen Markel kann man mit dem Verhalten 'Ankommen' minimieren.

Der Boid kommt an

Die Grundidee von 'Ankommen' besteht darin, unterhalb einer gewissen Mindestentfernung zum Ziel die gewünschte Geschwindigkeit zu verringern. Dies ist auf verschiedene Arten möglich. Z.B.

• lineare Anpassung
• Geschwindigkeitsberechnung abhängig vom restlichen Bremsweg und der Bremskraft

Für die zweite Variante werden die Gleichungen

• Kraft, Masse und Beschleunigung: F = m * a
• Geschwindigkeit, Beschleunigung und Zeit: v = v₀ + a * t mit v₀ = 0
• Weg, Beschleunigung und Zeit: s = 0.5 * a * t²

genutzt. Durch umformen und einsetzen kommt man zu : |v| = (2 * |s| * |F| / m)^0.5. Man erhält so eine (Grenz)Geschwindigkeit, mit der man bei gegebener Entfernung, Bremskraft und Masse noch zum Stand kommen kann. Im Programm wird allerdings mit der Beschleunigungskraft gerechnet. Da diese <= Bremskraft ist, passt es immer und der Weg ist 'schöner'.

Der Boid fängt ein Ziel ab

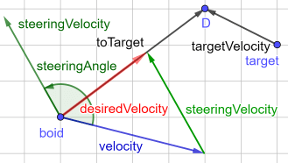
Vektoren für die Verfolgung

Das Verhalten 'Ziel ansteuern' liefert gute Ergebnisse für unbewegte oder langsame Ziele. Für schnell bewegte, entfernte Ziele ist der erzeugte Kurs zum Ziel nicht so gut, da er immer auf die aktuelle Position des Ziels ausgerichtet ist und daher im Allg. unnötig lang ist. Besser wäre es, wenn das Kursziel des Boids sofort auf die Position ausgerichtet wäre, an der sich das Ziel zum Zeitpunkt des Treffens befände. Diese Position ist aber unbekannt, da keine Information über den zukünftigen Kurs des Ziels vorhanden ist. Es bleibt nur, die Position des Ziels zu schätzen.
Zu diesem Zweck wird die minimale Zeit, die der Boid bis zur Zielposition braucht, berechnet. Unter der Annahme, daß das Ziel während dieser Zeit Richtung und Geschwindigkeit beibehält, wird die zukünftige Zielposition berechnet und der Kurs des Boids auf diese Position und nicht auf die aktuelle Position des Ziels ausgerichtet. Mit dieser Position wird dann genau so wie in 'Ziel ansteuern' verfahren.

• aktuelle Entfernung zum Ziel bestimmen: d = p_t - p_b
• Zeit für diese Strecke mit maximaler Geschwindigkeit berechnen: t = |d| / v_max
• zukünftige Position(D) des Ziel berechnen d'_t = p_t + v_t * t
• diese Position ansteuern

Der Boid flieht

Der Abstand zur aktuellen Position des Ziels soll maximiert werden. Fliehen ist daher das Gegenteil von Ansteuern. Das macht die Sache einfach. Es wird die selbe Berechnung wie bei 'Ansteuern' aufgeführt und das Ergebnis mit -1 multipliziert.

Der Boid entkommt

Entkommen ist 'Fliehen' entsprechend das Gegenteil von 'Abfangen'. Folglich wird die selbe Berechnung wie bei 'Abfangen' aufgeführt und das Ergebnis mit -1 multipliziert.

Der Boid bewegt sich ziellos

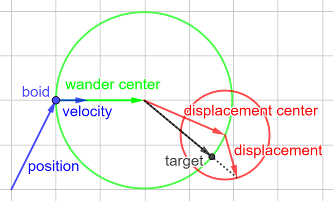
Vektoren für ziellose Bewegung

Die ziellose Bewegung läßt sich auf viele Arten realisieren. Wenn man jedoch komplett zufällige Richtungsänderungen erlaubt, sind beliebig viele große Richtungsänderungen möglich. Die sich daraus ergebenden zackeligen Wege erscheinen 'unglaubwürdig'. Um diese Schwäche zu verringern, müßte die Rotation bei Richtingsänderungen beschränkt werden. Besser ist daher eine Technik zu verwenden, bei der dieses Problem gar nicht erst auftritt. Dazu bietet sich folgende Möglichkeit an:
Der Boid 'schiebt' einen Kreis, den wander Circle, vor sich her. Darauf befindet sich ein weiter Kreis, der displacement Circle. Auf diesem wird zufällig ein Punkt ausgewählt. Dieser Punkt wird auf den wander Circle Radius projiziert. Der so erhaltene neue Punkt wird als target für den Kurs des Boids genutzt. Außerdem wird er der neue Mittelpunkt des displacement Circles. Dadurch erreicht man die Einschränkung der 'Zufalls'. Mit die Entfernung des wander Circles vom Boid und den Radien der beiden Kreise erhält man zusätzlich 3 Parameter, mit denen sich die Art des erzeugten Weges beeinflussen läßt.

• berechne wander center
• erzeuge random displacement
• berechne neues displacement center

Der Boid schwärmt in kombiniertem Verhalten

Um aus mehreren Boids einen Schwarm zu formen muss jeder Boid folgenden Regeln gehorchen.

• Bestimme die Boids deiner unmittelbaren Umgebung
• Bewege dich zum Schwerpunkt der Boids deiner unmittelbaren Umgebung. (Cohesion)
• Falls dir dein Nachbar zu nahe kommt, entferne dich von ihm. (Seperate)
• Bewege dich in der Richtung der Boids deiner unmittelbaren Umgebung. (Align)
• Bewege dich in die mittlere Richtung deiner Interessen

Jedes dieser Verhalten erzeugt einen (gewichteten) Vektor. Ihre Summe wird zur Berechnung der Steuerungskraft benutzt. Über die Gewichtung der Vektoren und die Größe der unmittelbaren Umgebung kann die Schwarmeigenschaft manipuliert werden. Leider wächst der Rechenaufwand quadratisch mit der Schwarmgröße. Es lohnt sich hier nach Optimierungsmöglichkeiten zu suchen.

Kommentar(e)