2D Vektoren

Was ist das?
In aller Kürze: Vektoren sind Zahlenlisten. 2D Vektoren haben immer 2 Komponenten.
Pro Dimension gibt es eine Komponente. Zahlen werden im Zusammenhang mit Vektoren Skalare genannt.
Vektoren haben Richtungen, Skalare nicht.
Die Komponeten können hinter- oder übereinander geschrieben werden. Sie sind dann Zeilen oder
Spaltenvektoren. Obwohl hier, der Technik wegen, die Zeilennotation genutzt wird, ist es angeraten
im echten Leben die Spaltennotation zu nutzen.
Vektoren können in zwei Komponentenarten ausgedrückt werden. Als
- X und Y Koordinatenpaar oder
- Länge und Richtung, wobei ein positiver Winkel als von der positiven X-Achse gegen den Uhrzeigersinn betrachtet wird. d.h. 300° = -60° und 380° = 20° bzw. 1,5π = -0,5π und 2,25π = 0,25π Es empfiehlt sich, grundsätzlich in Radiant zu rechen, weil das in den meisten Bibliotheken erwartet wird und man so viele Umrechnungen vermeiden kann.
Um sie von Koordinaten eines 2D Punktes zu unterscheiden, haben sich verschiedene Schreibweisen etabliert. Weit verbreitet ist die Schreibweise mit einem Pfeil über der Bezeichnung z.B. ⃗a. Es gibt auch die Schreibweise a z.B. im Zeichenprogramm und a. Hier wird im Zusammenhang mit Vektoren die Schreibweise a genutzt.
Geometrische Deutung.
-
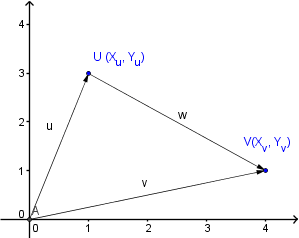
- Vektoren Typen
Hier bieten sich 3 Deutungen an. Nämlich als:
- Ortsvektor wie im Bild zu sehen, 'zeigt' der Vektor u auf den Punkt U. Die beiden Vektorkomponenten entsprechen den Koordinaten Xu und Yu von U. Damit haben Ortsvektoren ihren Anfang immer im Ursprung des Koordinatensystems.
- Verschiebungsvektor. Mit ihm lassen sich beliebige Punkte um Richtung und Länge des Verschiebungsvektors verschieben.
- Verbindungsvektor. w verbindet die Punkte U und V. w = V - U. Spitze - Anfang
Speziell ist der Nullvektor 0. Seine Komponenten sind 0. Entsprechend der oberen Deutung ist er als Ortsvektor der Ursprung, als Verschiebungsvektor neutral d.h. er macht nichts, als Verbindungsvektor die Verbindung eines Punktes mit sich selbst.
Mit Vektoren rechnen.
Multiplikation mit einem Skalar.
-
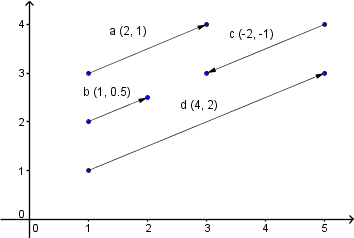
- Vektormultiplikation mit einem Skalar
Achtung: nicht verwechseln mit Skalarprodukt!
Multiplikation mit einem Skalar s:
w = s * u = (s * Xu, s * Yu)
Die Multiplikation erfolgt für jede Komponente. Das gilt auch für Division solange s ≠ 0.
Von a ausgehend ist im Bild
- b = a / 2.
- c = a * -1.
- d = a * 2.
Für alle Vektoren ist die neue Länge = alte Länge * bzw. / den Skalar. Je nach Vorzeichen
des Skalars zeigt der neue Vektor u.U. genau in die entgegengesetzte Richtung. Der neue Vektor ist immer parallel zum Alten.
Umgekehrt heißt das, zwei Vektoren sind genau dann parallel, wenn der eine ein Vielfaches des anderen ist.
d.h. Es gibt einen Skalar s ≠ 0 mit a = s * b bzw. a / s = b.
Ein 0 ist zu jedem Vektor parallel.
Für die Multiplikation mit einem Skalar gilt:
das distributiv Gesetz s * (u + v) = s * u + s * v bzw.
(m + n) * u = m * u + n * u
das assoziativ Gesetz m * n * u = m * (n * u) = n * (m * u)
Summe von Vektoren
-
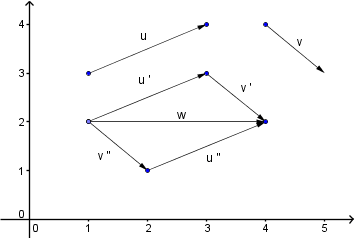
- Vektorsumme
Addition für Vektoren gleichen Typs d.h. 2D Vektor + 2D Vektor, 3D Vektor + 3D Vektor usw..
Die Addition (Subtraktion) erfolgt für jede Komponente. z.B.
w = u + v =
(Xu + Xv, Yu + Yv)
Durch Parallelverschiebung können die Vektoren u und v als
u' und v' oder v'' und u''
'aneinandergehängt' werden. Die Summe ist dann in beiden Fällen der resultierende Vektor
w. Was zeigt, daß die Vektoraddition unabhängig von der Reihenfolge ist.
Das Ganze funktioniert auch mit mehr als zwei Summanden. Nutzen lässt sich das z.B. bei Verschiebungen.
Sind, aus welchen Gründen auch immer, mehrere Verschiebungen angesagt, addiert man zuerst die
Verschiebungsvektoren, um schließlich den resultierenden Verschiebungsvektor anzuwenden. Damit kann
u.U. viel Rechenaufwand eingespart werden.
Für Summen gilt:
das kommutativ Gesetz: u + v = v + u
das assoziativ Gesetz: u + (v + w) = (u + v) + w
Kommt man bei der Summenbildung mehrerer Vektoren wieder beim ersten an, so ist die Summe ein 0.
Die Differenz u - v betrachten wir der Einfachheit halber
als u + (-v) und bedenken dabei, daß -v mit dem
selben Betrag genau in die entgegengesetzte Richtung von v zeigt. (Reihenfolge der Subtraktion ist nicht egal!) Das führt zu der Frage:
Was ist der Betrag eines Vektors?
Die Länge, der Betrag, eines Vektors ist die Wurzel der Summe der Quadrate seiner Komponenten. Im 2D Fall ist also
die Länge |u| = (Xu2 + Yu2)½ (Pythagoras).
Für den Betrag und Skalare gilt: |s * u| = |s| * |u|.
Bitte nicht auf Vektoren verallgemeinern. Für die gilt die Dreiecksungleichung
|u| + |v| ≥ |u + v| mit der Bedeutung:
der direkte Weg ist nicht länger als ein Umweg.
Das hängt eng mit den Verbindungsvektoren zusammen. Der Abstand der Punkte U und V entspricht |u - v|.
Was ist ein Einheitsvektor?
-
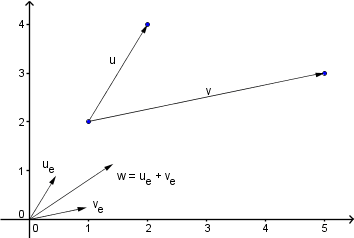
- Einheitsvektoren und Winkelhalbierende
Manchmal ist man nur an der Richtung interessiert, die Länge ist einem einerlei. Man kommt
zum Einheitsvektor ue von u mit:
ue = u / |u| mit: (|u| ≠ 0).
Dieser Vorgang wird Normalisieren genannt.
Wie der Name schon sagt, und die Gleichung für den Betrag zeigt, ist die Länge 1.
Die X Komponente von ue entspricht dem Cosinus des Winkels zwischen ue
und der X - Achse.
Die Y Komponente von ue entspricht dem Sinus des Winkels zwischen ue
und der X - Achse.
Sehr brauchbar ist das bei der Bestimmung der Winkelhalbierenden w der Vektoren
u und v. Die ist
w = ue + ve.
Wie man im Bild sieht, sind ue und ve gleich lang
und jeweils parallel zu u und v. Ihre Summe w halbiert
den von ue und ve eingeschlossenen Winkel und damit
auch den von u und v.
Aufteilung eines Vektors
Jeder 2D Vektor kann in 2 senkrecht aufeinander stehende Vektoren aufgeteilt werden. Dazu müssen
Basisvektoren eingeführt werden. Basisvektoren sind Einheitsvektoren, die parallel zu den
Achsen des Koordinatensystem liegen. Im 2D Koordinatensystem sind das eX = (1, 0)
und eY = (0, 1).
Die Aufteilung erfolg mit
u = Xu * eX + Yu * ey.
Auf diese Art kann jeder Vektor in die Linearkombination der Basisvektoren umgeformt werden. Das ist hilfreich,
wenn die X und Y Komponente unabhängig berechet werden wie z.B. bei einer ballistischen Flugbahn.
Was ist ein Vektorprodukt?
-
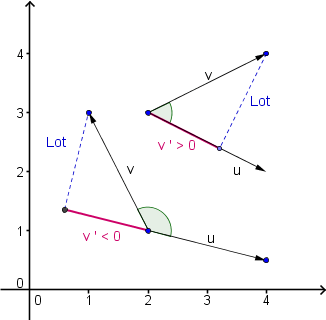
- Skalarprodukt von zwei Vektoren
Vielleich hat man schon mal die Begriffe Skalarprodukt und Kreuzprodukt gehört. Das Kreuzprodukt
ist für 2D nicht definiert und wird hier nicht behandelt. Für Skalarprodukt findet man auch
inneres Produkt. Es kommt zu seinem Namen, weil es aus 2 Vektoren einen Skalar macht. Sein Rechenzeichen
ist ·. Das Rechenzeichen für Kreuzprodukte ist ✕.
Das Produkt der beiden Vektoren berechnet sich nach:
v·u = vx*ux + vy*uy.
Wie berechnet sich der Winkel zwischen zwei Vektoren?
Betrachten wir ein Vektorenpaar und fällen das Lot von einem Vektor auf
den anderen. Die Länge v' (ein Skalar) der Projektion von v auf u ist proportional zum eingeschlossen Winkel.
(Daher auch die Bezeichnung inneres Produkt.)
Für spitze Winkel ist v' positiv, für stumpfe negativ.
Aus dem Cosinussatz lässt sich für das Skalarprodukt ableiten:
v·u = |v|*|u|*cos(φ)
Es ergeben sich drei Lösungen:
- v·u > 0 genau dann, wenn v und u einen spitzen Winkel bilden.
- v·u = 0 genau dann, wenn v und u senkrecht aufeinander stehen.
- v·u < 0 genau dann, wenn v und u einen stumpfen Winkel bilden.
Nach cos(φ) = v/|v|·u/|u| auflösen. Wegen ae = a / |a| umformen nach cos(φ) = ve·ue und φ = arccos(ve·ue). Bingo.
Wie dreht man einen Vektor?
-
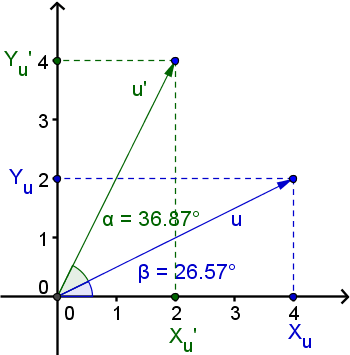
- Rotation eines Vektors
Der Vektor u soll um den Winkel α zu seiner neuen Position u'
gedreht werden. D.h. Der Punkt P(Xu, Yu) muss in den Punkt
P'(Xu', Yu') überführt werden.
Wegen der Kreisfunktionen (Einheitskreis) ergibt sich für:
- P(X, Y) = |u| * (cos(β), sin(β))
- P'(X', Y') = |u| * (cos(α+β), sin(α+β))
Wegen der Additionstheoreme
- sin(α+β) = sin(α) * cos(β) + cos(α) * sin(β)
- cos(α+β) = cos(α) * cos(β) - sin(α) * sin(β)
erhält man:
- X' = X * cos(α) - Y * sin(α)
- Y' = X * sin(α) + Y * cos(α)
In Matrixform lautet die Transformation
![]()
Sie erzeugt eine Drehung um den Winkel α gegen den Uhrzeigersinn.
Achtung: Eine Rotation dieser Art setzt Ursprungsvektoren voraus.
Ein beliebiger Vektor wird über eine entsprechende Translation zu einem Ursprungsvektor
gemacht. Im Anschluß wird die Rotationsmatrix angewendet. Auf deren
Ergebnis wird die umgekehrte Translation angewendet, um den Ergebnisvektor an den ursprünglichen
Herkunftsort zurückzuschieben.

